Calculus Integration How to Know Which to Use

The input before integration is the flow rate from the tap. This is the currently selected item.

Integration By Parts Integration By Parts Calculus Ap Calculus

That is L n L n and R n R n approximate the integral using the left-hand and right-hand endpoints of each subinterval respectively.

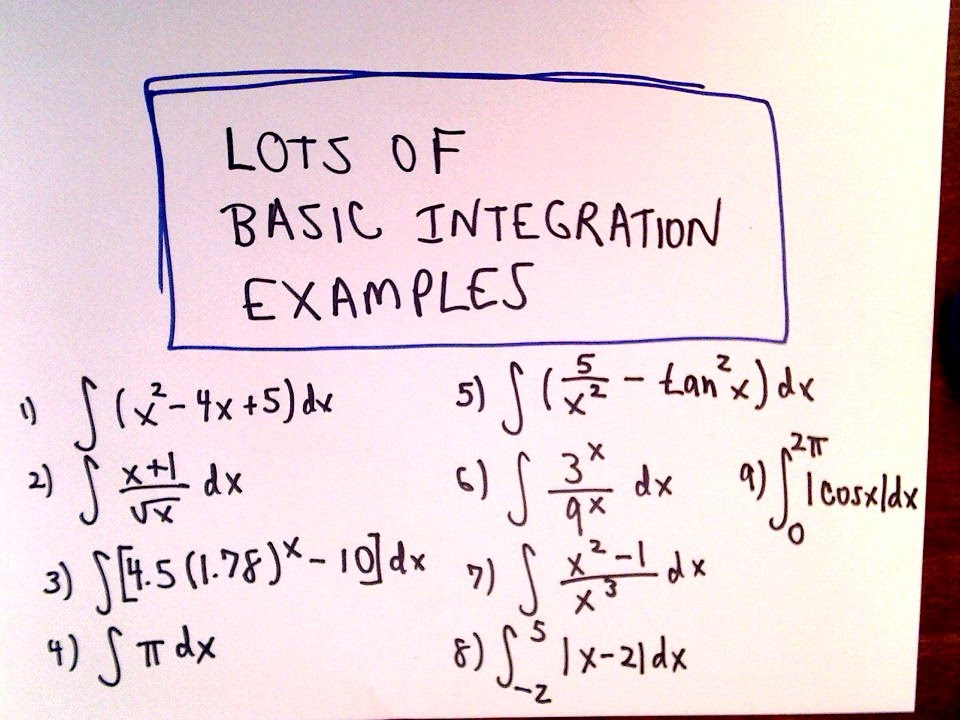
. FUN6 EU FUN6F LO FUN6F1 EK Google Classroom Facebook Twitter. If youre geared toward working in a mathematics and numbers-focused career youll certainly have to learn calculus as one of your required courses toward a higher education degree in programming machine learning gaming development and other learning. The process of finding integrals is called integrationAlong with differentiation integration is a fundamental essential operation of calculus and serves as a tool to solve problems in mathematics and.

Calculus analyses things that change and physics is much concerned with changes. You should also be familiar with algebraic transformations combinations compositions and inverses for general. The trapezoidal rule tends to overestimate the.

In this chapter we will give an introduction to definite and indefinite integrals. Integration is a way of uniting the part to find a whole. The bucket at right integrates the flow from the tap over time.

The integral of a function represents. These 2 derivatives are used to predict how a graph may look like the direction that it is taking on a specific point the shape of the graph at a specific. Using methods such as the first derivative and the second derivative a graph and its dimensions can be accurately estimated.

For example faced with Z x10 dx we realize immediately that the. So we wrap up the idea by just writing C at the end. Calculus differentiation integration etc.

The goal of indefinite integration is to get known antiderivatives andor known integrals. So this is essentially the formula for integration by parts. For physics youll need at least some.

The Calculus exam covers skills and concepts that are usually taught in a one-semester college course in calculus. Integration Strategy In this section we give a general set of guidelines for determining how to evaluate an integral. In addition a careful examination of Figure 315 leads us to make the following observations about using the trapezoidal rules and midpoint rules to estimate the definite integral of a nonnegative function.

Integration with partial fractions. In mathematics an integral assigns numbers to functions in a way that describes displacement area volume and other concepts that arise by combining infinitesimal data. There is no general chain rule for integration known.

Heres a simple example. The basic ideas are not more difficult than that. Youll often see it squared off in a traditional textbook.

The exam is primarily concerned with an intuitive understanding of. Is easier than you think. We know of a way to evaluate a definite integral using limits.

So this right over here tells us that if we have an integral or an antiderivative of the form f of x times the. It is often used to find the area underneath the graph of a function and the x-axis. We first learned of derivatives through limits and then learned rules that made the process simpler.

To get chain rules for integration one can take differentiation rules that result in derivatives that contain a composition and integrate this rules once or multiple times and rearrange then. The fundamental theorem of calculus is a theorem that links the concept of differentiating a function calculating the gradient with the concept of integrating a function calculating the area under the curve. Integration with partial fractions.

We will discuss the definition and properties of each type of integral as well as how to compute them including the Substitution Rule. The most common practical use of calculus is when plotting graphs of certain formulae or functions. The inverse process of finding derivatives is finding the integrals.

The content of each exam is approximately 60 limits and differential calculus and 40 integral calculus. The key feature of this theorem is its connection between the indefinite integral. Sometimes we can work out an integral because we know a matching derivative.

Math APCollege Calculus BC Integration and accumulation of change Integrating using linear partial fractions. So Im just switching the sides just to give it in a form that you might be more used to seeing in a calculus book. The two operations are inverses of each other apart from a constant value which is dependent on where one starts to compute area.

In the next section we will see how the Fundamental Theorem of Calculus makes the process simpler. Algebraic trigonometric exponential logarithmic and general functions are included. The guidelines give here involve a mix of both Calculus I and Calculus II techniques to be as general as possible.

The first rule to know is that integrals and derivatives are opposites. Let us use a tap to fill a tank. Integration can be used to find areas volumes central points and many useful things.

Integrating using linear partial fractions. The first part of the theorem sometimes. For example as a statistician you would need to know calculus to analyze changes in data in statistical programs.

Thus integration is the inverse of differentiation. The flow is the time derivative of the water in the bucket. Integral calculus helps in finding the anti-derivatives of a function.

So I will do the same. So when we reverse the operation to find the integral we only know 2x but there could have been a constant of any value. I will square it off.

The process of finding the anti-derivative of a function is called integration. In particular you should understand the properties of linear polynomial rational exponential logarithmic trigonometric inverse trigonometric and piecewise-defined functions and know how to graph these functions and solve equations involving them. Sometimes this is a simple problem since it will be apparent that the function you wish to integrate is a derivative in some straightforward way.

In the integral calculus we find a function whose differential is given. Integration is used to define and calculate the area of the region bounded by the graph of functions. We will give the Fundamental Theorem of Calculus showing the relationship between derivatives and integrals.

Techniques of Integration Over the next few sections we examine some techniques that are frequently successful when seeking antiderivatives of functions. We will also discuss the Area Problem an. The area of the curved shape is approximated by tracing the.

These anti-derivatives are also called the integrals of the function. Also note that there really isnt one set of guidelines that will always work and so you always need to be.

Introduction To Integration Integral Calculus Calculus Math Formulas Differential Calculus

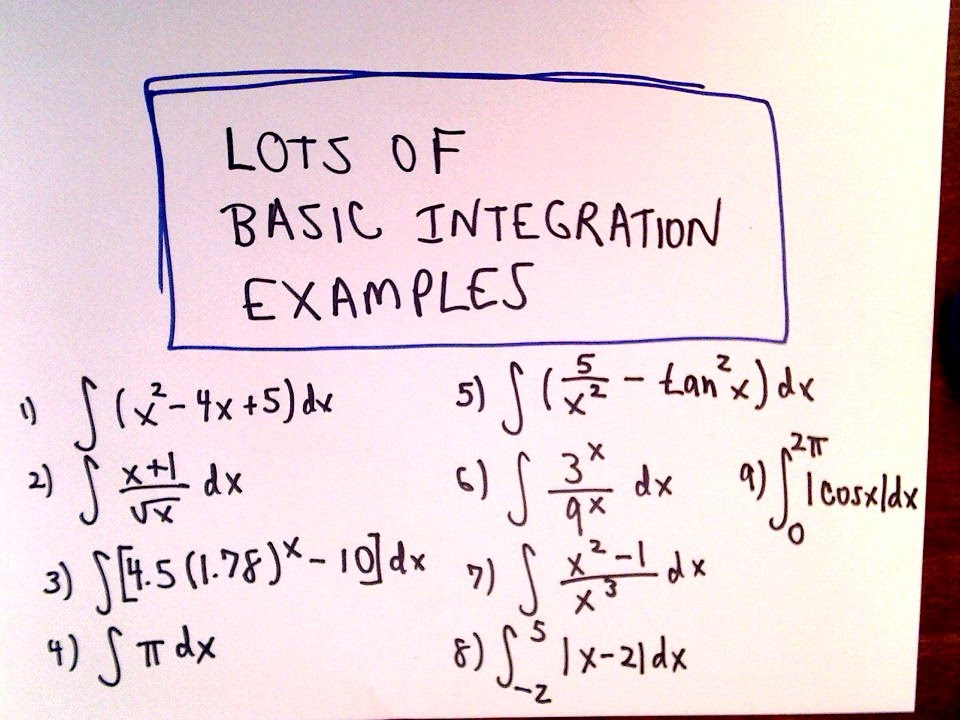
Lots Of Basic Antiderivative Integration Integral Examples Integrity Basic Calculus

Integration Flow Chart New A Level How Can I Integrate That Teaching Resources Flow Chart Math Methods Math Formulas

Calculus Applications To Integration Graphic Organizer And Poster Calculus Ap Calculus Graphic Organizers